Modeling Calcium Concentration and Biochemical Reactions
urn:nbn:de:0009-3-2245
Abstract. Almost all regions of the brain receive one or more neuromodulatory inputs, and disrupting these inputs produces deficits in neuronal function. Neuromodulators act through intracellular second messenger pathways to influence the electrical properties of neurons, integration of synaptic inputs, spatio-temporal firing dynamics of neuronal networks, and, ultimately, systems behavior. Second messengers pathways consist of series of bimolecular reactions, enzymatic reactions, and diffusion. Calcium is the second messenger molecule with the most effectors, and thus is highly regulated by buffers, pumps and intracellular stores. Computational modeling provides an innovative, yet practical method to evaluate the spatial extent, time course and interaction among second messenger pathways, and the interaction of second messengers with neuron electrical properties. These processes occur both in compartments where the number of molecules are large enough to describe reactions deterministically (e.g. cell body), and in compartments where the number of molecules is small enough that reactions occur stochastically (e.g. spines). – In this tutorial, I explain how to develop models of second messenger pathways and calcium dynamics. The first part of the tutorial explains the equations used to model bimolecular reactions, enzyme reactions, calcium release channels, calcium pumps and diffusion. The second part explains some of the GENESIS, Kinetikit and Chemesis objects that implement the appropriate equations. In depth explanation of calcium and second messenger models is provided by reviewing code, both in XPP, Chemesis and Kinetikit, that implements simple models of calcium dynamics and second messenger cascades.
Keywords: Biochemical reactions, calcium, modeling, simulation, GENESIS, diffusion, second messengers, enzymes, neuromodulators
Almost all regions of the brain receive one or more neuromodulatory inputs, and disrupting these inputs produces deficits in neuronal function. One example is Parkinson’s disease, a degenerative disorder of the dopaminergic system in the basal ganglia, which affects as many as 10% of people over 60. The lack of dopamine input to the basal ganglia produces abnormalities in voluntary motor activity ( Wichmann and DeLong 1998 ): Parkinsonian patients exhibit difficulty initiating movements, poorly controlled movements, and shuffling gait. Another example of the importance of neuromodulators is the role of acetylcholine in the hippocampus. Blocking the muscarinic acetylcholine receptor disrupts acquisition of context memory ( Gale et al. 2001 ). Though the importance of neuromodulation is widely acknowledged, the mechanisms of neuromodulatory action are not completely understood.
Neuromodulators act through intracellular second messenger pathways to influence the electrical properties of neurons. Neuromodulators may modify gene expression, produce plasticity of various synaptic channels, or modify properties of voltage dependent channels, depending on both the specific neuromodulator and the target neuron. Channel modulation shapes electrophysiological integration of neuronal inputs, spatio-temporal firing dynamics of neuronal networks, and, ultimately, systems behavior. For example, dopamine modulates several voltage dependent and synaptic channels of striatal spiny projection neurons; the lack of dopamine alters the firing dynamics of these neurons and the striatum as a whole. In contrast to traditional synaptic transmission, the time course of neuromodulation is slow and prolonged. Also, due to activation of diffusible second messengers, the action of neuromodulators may be relatively widespread and distant from the synapse. Neuromodulator interactions may be synergistic or antagonistic depending on the time course of the activated second messenger reactions (e.g. Bhalla and Iyengar 1999 ; Leloup and Goldbeter 1999 ). Consequently, the complexity of second messenger pathways constitute a formidable obstacle to the complete understanding of neuromodulatory effects.
Calcium is one of the most important second messenger molecules, with a diverse array of effectors. Calcium directly moderates electrical activity, on a relatively fast time scale, through its control of calcium dependent potassium channels. Long term effects are mediated by various kinases and phosphatases. Calcium is one of the activators of protein kinase C, which plays a role in synaptic plasticity. In a complex with calmodulin, calcium is an activator or regulator of several enzymes, including calcium-calmodulin dependent protein kinase, which plays a role in synaptic plasticity, and adenylate cyclase, which produces cAMP, another important second messenger. Neurons have numerous sources and sinks of calcium in order to tightly control this very active molecule. Sources include voltage dependent calcium channels (which allows electrical activity to moderate calcium concentration) and intracellular stores; sinks include buffers and membrane pumps.
Second messenger pathways, and some mechanisms controlling calcium concentration, are modeled as a series of bimolecular reactions, enzymatic reactions, and diffusion. These processes occur both in compartments where the number of molecules are large enough to describe reactions deterministically (e.g. cell body), and in compartments where the number of molecules is small enough that reactions occur stochastically (e.g. spines). Thus, to model and simulate second messenger pathways in neurons requires algorithms for both diffusion and reactions, both deterministic and stochastic. This mesoscopic modeling approach is required because microscopic processes (e.g. reactions in spines) influence macroscopic behavior (e.g. calcium concentration in the dendrite). This tutorial reviews the biochemical reactions and mathematical equations used to describe and model deterministic second messenger pathways. In addition, calcium pumps and calcium release channels also are described.
These are stoichiometric interactions between substrate molecules to form product molecules. Bimolecular reactions usually involve formation of a bond between the substrate molecules. A stoichiometric interaction implies that the reaction specifies the number of each molecule type required for the reaction, e.g. one hydroxy ion plus one hydrogen atom create one water molecule. This stoichiometry implies that molecules are consumed in order to make the product.
The reaction order is the number of simultaneously interacting molecules. In a first order reaction, such as radioactive decay, a single substrate becomes the product (Eq.1). The rate constant is the rate (units of per sec) at which substrate becomes product.
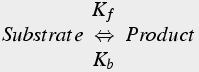
(1)
The ratio of backward rate constant to forward rate constant gives the concentration of substrates and products at equilibrium (Eq.2), i.e., when there is no net change in concentration over time.
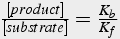
(2)
These reactions are modeled with differential equations (Eq.3) that express the rate of change of molecule quantity with respect to time. The rate constants give the frequency of transitions between substrates and products.
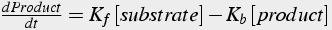
(3)
In closed systems, mass is conserved, thus, one of the differential equations can be replaced with an algebraic equation stating the amount of substrate remaining is its initial value minus the amount of product (substrate = initial value –product).
In a second order reaction, each molecule of product requires 1 molecule of one substrate and 1 molecule of another substrate (or two molecules of a single substrate). In other words, two molecules must collide for the reaction to occur (Eq.4).
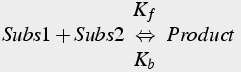
(4)
Again, differential equations express the rate of change of molecule quantity (Eq.5). The forward rate constant has units of per sec per mole (or equivalent units).
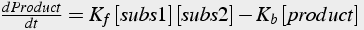
(5)
Conservation of mass can be applied to both substrates to generate algebraic equations (Eq.6) describing the amount of substrate remaining given initial values:
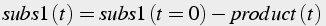
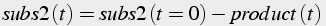
(6)
Third and higher order reactions can be described: the order of the reaction is the number of substrate molecules required for the product (Eq.7).
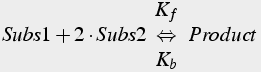
(7)
The differential equation describing the rate of change of product (Eq.8) is the forward rate constant times all the substrates minus the backward rate constant times all the products (if more than one).
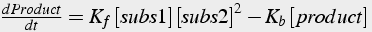
(8)
If two molecules of one substrate are consumed in the reaction, then, in the conservation equations, the amount of substrate decreases twice as fast as product increases (Eq.9).
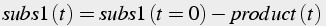
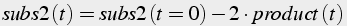
(9)
It is unlikely that collisions among three molecules ever occur simultaneously, thus, differential equations describing these higher order reactions are approximations of the series of second order reactions occurring to produce a multi-substrate molecule.
It is important to note that these equations describe the behavior of large number of molecules (mass action kinetics). If only small numbers of molecules are present within a compartment, stochastic equations are required to accurately describe the random occurrence of transitions.
Enzyme reactions are special types of two step reactions in which the enzyme is regenerated in the second step. Thus, enzyme is not consumed, and each enzyme molecule can make multiple product molecules (Eq.10).
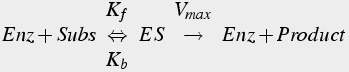
(10)
Deriving the differential equations (Eq.11) involves (1) writing one equation for each unknown, and (2) including terms describing each path leading toward and away from each molecule. Initial values of both enzyme and substrate must be given.
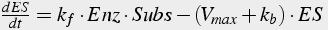
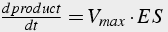
(11)
Under certain conditions, known as the Michaelis-Menten conditions, the equations can be simplified (Eq.12). These conditions are that the backward reaction rate for the second step is zero; the quantity of the enzyme-substrate complex rapidly reaches equilibrium, and that the amount of substrate is in excess (the enzyme quantity is rate limiting).
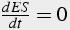 ,
,
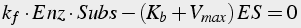
(12)
When these conditions are satisfied, the equation describing the quantity of enzyme-substrate complex can be solved in steady state (Eq.13-15):
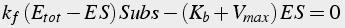
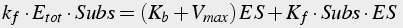
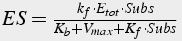
(13)
Divide top and bottom by Kf
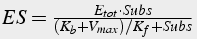
(14)
Substitute ES into equation 11 for product:

(15).
Second messenger pathways are composed of a cascade of biochemical reactions. The product of one reaction is the substrate or enzyme of subsequent reactions. One measure of the likelihood a reaction occurring is the affinity. The higher the affinity, the lower the concentration of substrate needed for the reaction to proceed. The affinity of a bimolecular reaction is kB/kF; the affinity of an enzyme reaction is kM.
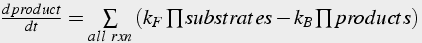
(16)
To model a cascade of biochemical reactions it is important to write one equation (either differential equation of conservation of mass equation) for each molecule, form of the molecule, or molecule complex (Eq.16). In addition, the right hand side of the differential equation must include terms describing all reactions that will increase or decrease the quantity. Note that some molecules may act as a product in one reaction / equation and a substrate in another reaction / equation.
In neurons, second messenger pathways are required when modeling metabotropic receptors. These receptors differ from ionic receptors in that the protein does not form the ionic channel. Instead the receptor protein is linked to a GTP binding protein, meaning that when the neurotransmitter binds, the receptor acts as an enzyme that activates the G protein. Effects of metabotropic receptors are mediated either by the activated G protein subunits or by down stream second messengers produced by a cascade of biochemical reactions (see Nicholls 2001 Fig. 10.1, p.178). GTP binding proteins, or G proteins, are composed of three subunits: the α subunit, Gα, the β subunit, and the γ subunit. The Gα binds to either GDP or GTP; the β and γ subunits remain in a complex known as Gβγ. In the inactive form, the Gα subunit is bound to GDP, and all three subunits remain in a complex together. When a metabotropic receptor binds to an agonist, the complex acts as an enzyme which catalyzes the exchange of GDP for GTP. The GαGTP subunit separates from the Gβγ complex, both of which can activate target proteins (see Nicholls 2001 Fig. 10.3, p.180).
In some cases, the Gβγ directly binds to and gates ionic channels. In other cases, the GαGTP subunit binds to an enzyme, which produces a diffusible second messenger, which then binds to an enzyme called a kinase, which phosphorylates various target molecules such as ion channels (see Nicholls 2001 Fig. 10.4 b, p.182).
One example of a second messenger pathway involving the Gα subunit is the β noradrenergic receptor. The particular Gα subunit linked to this receptor activates adenylyl cylcase when it is bound to GTP. Adenylyl cylcase produces cAMP, which activates protein kinase A. One of the targets of protein kinase A is a voltage activated calcium channel. When protein kinase A puts a phosphate on this channel, it becomes available for activation. Thus, protein kinase A does not activate the channel, but effectively increases the number of channels that can be activated when the neuron depolarizes (see Nicholls 2001 Fig. 10.10, p.186).
Opposing the action of metabotropic receptors are other enzymes, such as protein phosphatases which remove phosphate groups from molecules, and phosphodiesterase which breaks down cAMP and cGMP (see Nicholls 2001 Fig. 10.13, p.189). Another norepinephrine receptor is coupled to a Gα subunit which activates phospholipase C. Phospholipase C produces diacyl glycerol (DAG) and inositol triphosphate (IP3) from a membrane phospholipid known as PIP2. IP3 diffuses in the cytosol and can activate calcium channels located on the endoplasmic reticulum. DAG diffuses within the membrane, and can activate protein kinase C, another enzyme that phosphorylates ionic channels.
When the metabotropic glutamate receptor binds to glutamate, it becomes an active enzyme that catalyzes the activation of the Gq variety of G protein. The Gqα activated subunit binds to and activates PLC, which catalyzes the production of IP3 from PIP2.
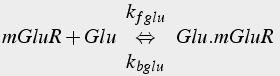
(17a)
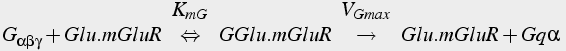
(17b)
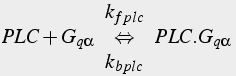
(17c)
The production of IP3 is inactivated at two points of the pathway. The Gq αGTP is inactivated by hydrolysis of the GTP to GDP (Eq. 18). Also, IP3 is inactivated by degradation.
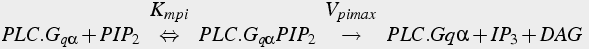
(18a)
Degradation:
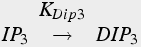
(18b)
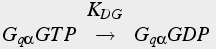
(18c)
The biochemical reactions are converted into differential equations (Eq. 19, 20) using the method described above. Reaction 2 includes terms from three different reactions: production (using the Michaelis-Menten formulation), hydrolysis of Gq α, and binding to PLC.
Reaction 1:
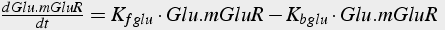
(19)
Reaction 2 (enzyme) and degradation:
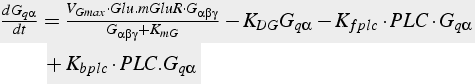
(20)
Equations 21 and 22 do not use the Michaelis-Menten assumption for these enzyme reactions. Equation 21 has terms for binding of Gq α to PLC, and also binding of PIP2. Equation 22 has terms for production and degradation of IP3.
Reaction 3 (non-MM enzyme formulation):
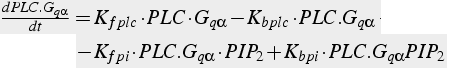
(21)
Reaction 4 (non-MM enzyme) and degradation:
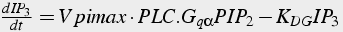
(22)
These equations are implemented in Tutorial05.g . Tutorial05.g uses additional files as described in the supplementary material section “ Article Resources ”.
Calcium is one of the most important intracellular second messengers and has a wide range of actions (Fig. 1). When bound to calmodulin, it can activate several key enzymes, such as calcium-calmodulin dependent protein kinase (CamKinase), some forms of adenylyl cylcase and phosphodiesterase, and calcineurin. Together with diacylglycerol, it can activate protein kinase C. It gates various calcium dependent potassium channels, and can inhibit phospholipases.
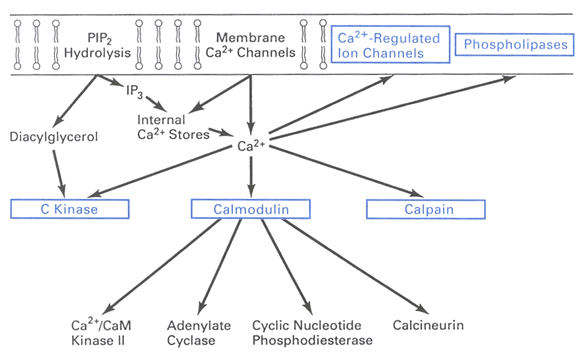
Figure 1: Calcium sources, sinks, and actions. Reprinted from Levitan and Kaczmarek (1997), Fig. 12-16, redrawn from Kennedy (1989) , Fig.1. With kind permission from Elsevier and Oxford University Press. For details see text.
Due to its importance, there are many molecules and subcellular structures involved in its regulation. One means of increasing the calcium concentration inside the cell is influx through calcium channels. Calcium is pumped out of the cells by pumps on the plasma membrane, and on the smooth endoplasmic reticulum (SER). One of the plasma membrane pumps requires ATP to extrude calcium, the other pump uses the sodium concentration gradient as energy to extrude calcium. The pump on the SER uses ATP, and maintains the SER as an internal store of calcium. The calcium within the SER can be released to produce an increase in intracellular calcium concentration. The release occurs through one of two types of calcium permeable channels on the SER. One of the channels is activated by IP3 and calcium; the other channel, for which ryanodine is both an agonist and antagonist, is activated by calcium alone. Buffers are cytoplasmic protein molecules which bind calcium, thereby decreaseing free calcium concentration and prevent it from activating other molecules. Diffusion is the means whereby calcium ions move from one location to another. Diffusion tends to decrease calcium near its source, but increase calcium further away.
Calcium concentration is coupled to electrical activity of neurons through calcium permeable channels. In response to depolarization, calcium channels open, and calcium flows in. The influx depends on the difference between the membrane potential and the reversal potential (known as driving potential) and the number of open calcium channels (Fig. 2).
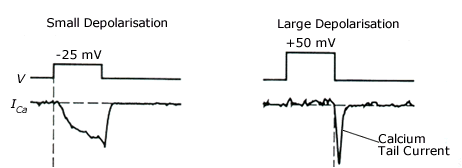
Figure 2: Calcium influx is influenced by driving potential; thus with a large depolarization, the influx is large during initial repolarization. Reprinted from Levitan and Kaczmarek (1997), Fig 9-7b, adapted from Augustine (1985) , Fig. 1. With kind permission from the Journal of Physiology and Oxford University Press. For details see text.
Thus a small depolarization produces a small number of open channels, but the large driving potential produces a significant calcium current. A large depolarization produces a large number of open channels, but the small driving potential prevents influx of calcium. Once the depolarization is released, the calcium channels stay open for a brief time with a large driving potential, thus calcium influx is large at the ”tail“ of the depolarization.
The Calcium influx is usually implemented using the following equations (Eq.23-25):
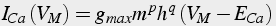
(23)
Ideally, you should use the Goldmann-Hodgkin-Katz Equation:
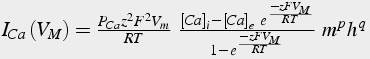
(24)
Influx due to calcium current is calculated by:
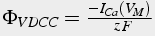
(25)
where F is Faraday's constant, R is the ideal gas constant, T is temperature, and z is valence. The negative sign is because inward current is negative.
Calcium diffusion is movement of calcium ions from an area of high concentration to an area of low concentration. Diffusion is also used to describe the ”flow“ of heat from hot areas to cold areas. Diffusion is described quantitatively using partial differential equations, and the derivation of the equation provides an intuitive feel for the parameters influencing the rate of movement. The simplest case is diffusion through a cylinder under the assumption that all movement is in the axial direction, there is no movement radially or tangentially (Fig. 3).
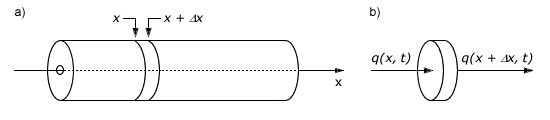
Figure 3: a) Cylinder, showing slice of width Δx, used to derive the diffusion equation ; b) Left and right surface areas of cylinder slice showing heat fluxes. After Powers (1979) . For details see text.
First we examine the flux into and out of a slice of the cylinder of width Δx (Fig. 3). The flux into the slice from the left at time t is called q(x,t). The flux out of the slice at the right is called q(x+Δx,t). If the flux is going in the opposite direction from what we specified, the fluxes will be negative. We assume there is no production or consumption of calcium within the slice. In other words, there are no pumps, or calcium channels. The flux is specified as quantity of molecules per unit surface area (Eq. 26-31). The area of the cylindrical slice, through which the molecules move, is called A. Thus the total influx of molecules is A q(x,t), and the total outflux of molecules is A q(x+Δx,t). The difference between influx and outflux produces an accumulation of molecules, which can increase or decrease the concentration, C, which is molecules (or moles) per unit volume.
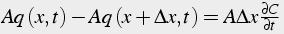
(26)
Divide both sides by A and Δx:
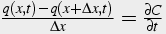
(27)
The limit of the left hand side as Δx -> 0:
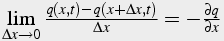
(28)
Thus,
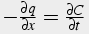
(29)
Apply Flick’s Law for diffusion and substitute RHS into original equation
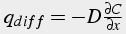 ,
,
(30a)
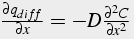 ,
,
(30b)
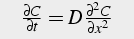
(31)
Thus, the flux difference is equal to the concentration change times the slice volume, which is A Δx. In a dendrite, which is roughly cylindrical, diffusion may be radial – flowing from spines and calcium channels toward the center of the dendrite (Fig. 4).
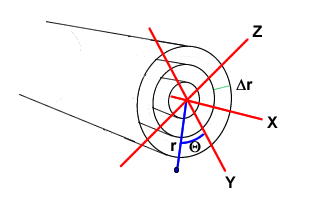
Figure 4: Subdivision of three dimensional cylinder into rings for axial and radial diffusion. Adapted from DeSchutter and Schmolen (1998) . For details see text.
Thus, we model calcium as flowing both axially in the x direction, and radially between rings of thickness Δr. The net movement of calcium is from areas of high concentration to areas of low concentration. The change in concentration over time is proportional to the calcium gradient in space and the diffusion coefficient. Depending on the geometry / morphology of the neuron, the spatial calcium gradient is in one or two (or even three) dimensions (Eq. 32-34).
One dimensional Diffusion Equation:
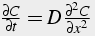
(32)
Two dimensional Diffusion Equation (radial coordinates):
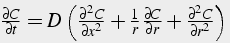
(33)
Though the diffusion equation can be solved analytically under some conditions, to implement diffusion in a neuron with calcium channels, pumps and other regulatory mechanisms, a compartmental or discrete form of the equation is used (Eq. 34, Fig. 5).
1-D and 2-D diffusion:
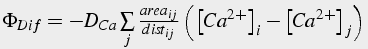
(34)
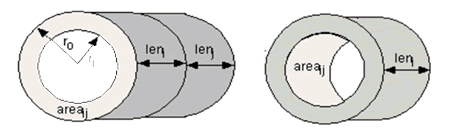
Figure 5: Diffusion in the axial Dimension (left): Distance: distij = (leni + lenj)/2 and surface area: areaij = π (ro 2-ri 2). Diffusion in the radial dimension (right): Distance: distij = (thicko +thicki)/2 and surface area: areaij = 2πrileni.
Calcium is stored within the smooth endoplasmic reticulum (SER) and can be released to produce an increase in intracellular calcium concentration (Fig. 6). In contrast to voltage dependent calcium channels on the plasma membrane, calcium permeable channels on the SER are gated by second messengers and intracellular calcium concentration. The IP3 receptor channel requires IP3, which is produced when phospholipase C cleaves the membrane phospholipid phosphoinositol bisphosphate.
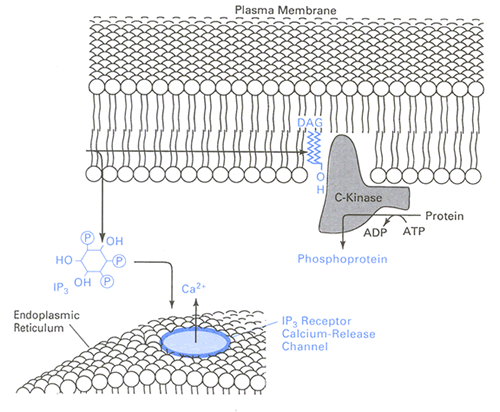
Figure 6: Calcium permeable channels on the ER are gated by IP3, produced by cleavage of plasma membrane phospholipids. Reprinted from Levitan and Kaczmarek (1997) , Fig 12-13a, adapted from Berridge (1987) , Fig. 1. With kind permission from Annual Reviews and Oxford University Press. For details see text.
These calcium release channels are described using Markov kinetic models. The channel is a multimeric molecule with each subunit having mutliple states or conformations. One of the states is the open state, and the remaining are closed and non-conducting. The transitions between states are governed by the transition rate constants. The forward rate constants depend on calcium, or, for the IP3 receptor channel, they depend on IP3 concentration. The backward rate constants, representing the dissociation of calcium or IP3, are independent of concentration. One of models of calcium release channels assumes there are two calcium binding sites on each subunit of the IP3 and ryanodine receptor channels. Calcium bound to one of the binding sites allows the channel to open with relatively fast kinetics; binding at the second calcium binding site causes the channel to close with relatively slow kinetics. The IP3 receptor channel has an additional IP3 binding site, which binds IP3 with fast kinetics. If the rate of binding IP3 is independent of the number of calcium ions binding, and if the calcium ion binding sites are independent of each other, the 8 state model of De Young and Keizer ( DeYoung and Keizer 1992 ) results (Fig. 7).
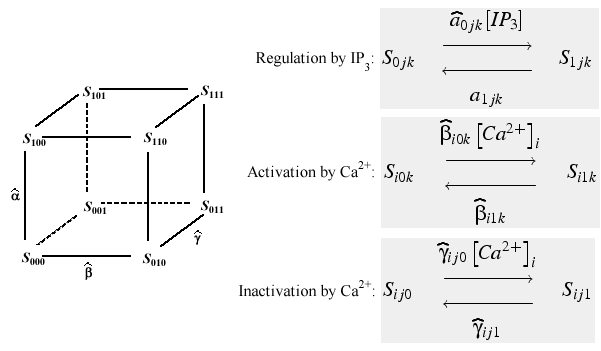
Figure 7: Eight state model developed by DeYoung and Keizer (1992 ), Figure redrawn from Li and Rinzel (1994 ).
This model of the IP3 receptor channel has only six independent rate constants. An analogous model of the ryanodine receptor channel was developed by Tang and Othmer (Tang and Othmer 1994) (Fig. 8):
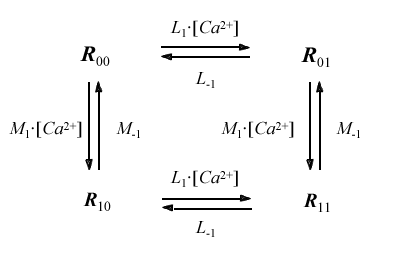
Figure 8: Model of the ryanodine receptor channel analogous to IP3 receptor developed by Tang and Ottmer (1994) .
Binding calcium at one site proceeds quickly (rate L1) and causes the channel to open, binding calcium at the second site is relatively slow (rate M1) and causes the channel to close.
Calcium flow through these release channels is similar to that for plasma membrane ion channels. Single channels open and close randomly (Fig. 9).
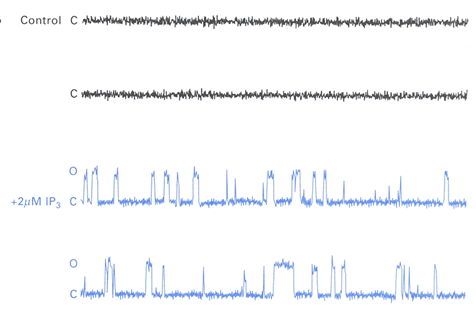
Figure 9: Single channel calcium current through IP3 receptor channels is gated by IP3. Reprinted from Levitan and Kaczmarek (1997) , from an experiment by Barbara E. Ehrlich and colleagues. With kind permission from Barbara E. Ehrlich (Yale University) and Oxford University Press. For details see text.
The flow of calcium ions through the open channels is proportional to concentration difference between the ER and the cytosol. The flow of calcium ions also is proportional to the fraction of channels in the open state. If there are n independent subunits, then the fraction of open channels depends on the fraction of ”open“ subunits, X, raised to the nth power (Eq.35).
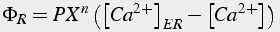
(35)
Where P is permeability, X is fraction of channels in open state, n is number of independent subunits.
The dynamics of the calcium release channel are similar to the voltage dependent sodium channel. In the presence of IP3, calcium plays the role of membrane potential. A small calcium concentration produces a small fraction of open channels. These open channels allow calcium flow, which raises the calcium concentration. The larger calcium concentration causes a larger fraction of open channels. This is a positive feedback loop, which leads to rapid increase in calcium, similar to the positive feedback loop with the sodium channel producing a rapid increase in membrane potential. The high calcium concentration also causes a slower channel inactivation which limits the peak calcium. The inactivation is analogous to sodium channel inactivation. The net result of the positive and negative feedback loops is a calcium spike. The calcium concentration returns to basal level through the action of pumps, which returns calcium back to the ER. These dynamics are similar enough to the voltage dependent sodium channel that they can be modeled using analogous equations (Eq.36-38).
Hodgkin Huxley like equations to describe IICR ( Li and Rinzel 1994 ):

(36)
Fast, time independent activation by calcium and IP3
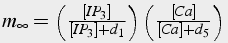
(37)
Slow, time dependent inactivation
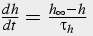
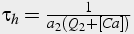 ,
,
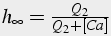
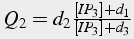
(38)
The change in calcium concentration is proportional to m3, fast activation by calcium and IP3, and h3, slow inactivation by calcium. A first order differential equation describes the change in h, whereas m is solved in steady state because it changes significantly faster than h.
Calcium pumps and buffers oppose the actions of calcium channels. They remove free calcium from the intracellular space. The plasma membrane calcium ATPase pump (PMCA) extrudes calcium into the extracellular space. It binds one calcium ion for each ATP molecule used, it has a high affinity, ~300 -600 nM, but low capacity ( Enyedi et al. 1994 ). The smooth endoplasmic reticulum calcium ATPase pump (SERCA) sequesters calcium in SER. It binds two calcium ions for each ATP molecule used, and also has a high affinity of ~100 nM. These pumps act similar to enzymes: a reversible stage, in which calcium binds to the pump, is followed by an irreversible stage, in which the pump changes conformation and transports the calcium ion. The equations for these pumps use the Michaelis-Menten enzyme formulation (Eq.39) solved in steady state.
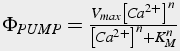
(39)
Vmax is the maximal pump capacity, n is the Hill coefficient: number of calcium molecules bound, KM is the affinity (half maximal concentration).
A Michaelis-Menton pump will decrease calcium to 0, below the resting calcium of neurons (Eq.40, 41). It is assumed that, at the resting calcium concentration, the effect of the pumps is balanced by leak into the cytosol from the ER (for SERCA) and from the extracellular space (for PMCA).
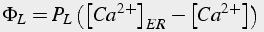
(40)
where
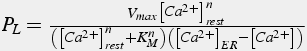
(41)
This leak is modeled as a constant times the concentration gradient. The value of the constant is obtained by setting the leak flux equal to the pump flux.
One additional calcium ”pump“ is the sodium calcium exchanger. It removes one calcium ion for each three (possibly 4; Fujioka et al. 2000 ) sodium ions (see also Nicholls 2001 Fig. 4.4 b, p.68). This produces a net charge transfer of one proton for each transport cycle. The positive charge transfer produces a small depolarization. This pump has a lower affinity than the PMCA, but it has a much greater capacity, as much as 50 times greater. Because the exchanger depends on the sodium concentration gradient, it is possible to reverse the direction of the pump, either by depolarization of the neuron, an increase in internal sodium concentration, or a decrease in external sodium concentration.
There are many formulations for this pump. The one presented ( Gall et al. 1999 ) calculates calcium flux from the exchanger current (Eq.41). The exchanger current depends on the driving potential, and the affinity of the exchanger for calcium. The driving potential is calculated from the reversal potential of the pump which depends on both the calcium and sodium concentration gradients.
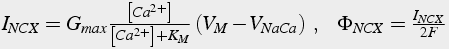
(42a)
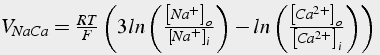
(42b)
Buffers are protein molecules that bind calcium ions, thus they are modeled using bimolecular reactions, as explained earlier. Not only calcium concentration, but also buffer concentration must be modeled. If diffusible buffers are present, then additional diffusion equations (Eq.43, 44) for the buffers are required.
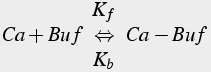
(43)
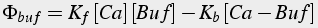
(44)
Pumps, buffers, diffusion, channels all contribute to modify calcium concentration. The equations for each of these mechanisms calculate the change in calcium with respect to time. The net change in calcium concentration is obtained by summing all the flux terms, and then dividing by volume. It is extremely important that all flux terms are in units of moles (not concentration), and then flux is divided by volume to obtain concentration after the summation. The concentration of calcium in the ER is calculated in the same manner, but some of the flux terms are different (Eq.45).
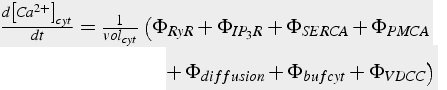
(45a)
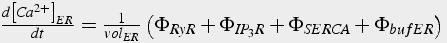
(45b)
To model in calcium dynamics using XPPAUT, implement the equations shown here (for more information on XPPAUT, see Ermentrout 2002 and www.math.pitt.edu/~bard/xpp/xpp.html); to model calcium dynamics in NEURON, see ( Hines and Carnevale 2000 ); to model calcium dynamics in GENESIS, use various objects as explained below.
Modeling these calcium mechanisms using Chemesis (for details see the Chemisis Download Page ) is illustrated in several tutorials, which build sequentially. Cal1.g shows how to model calcium buffering. Cal2.g adds a second compartment to demonstrate diffusion between two different compartments, the morphology of which is illustrated in figure 10. Cal3.g adds release from intracellular stores through the IP3 receptor channel, as illustrated in figure 11. The lack of a pump means that calcium dynamics are unbalanced, and cannot be maintained at resting levels. Cal4.g adds the SERCA pump (also shown in figure 11), a calcium sink to balance the calcium source. All cal<n>.g files use additional files as described in the supplementary material section “ Article Resources ”.
Figure 10: Morphology of model cell used in Cal2.g, Cal3.g, Cal4.g.
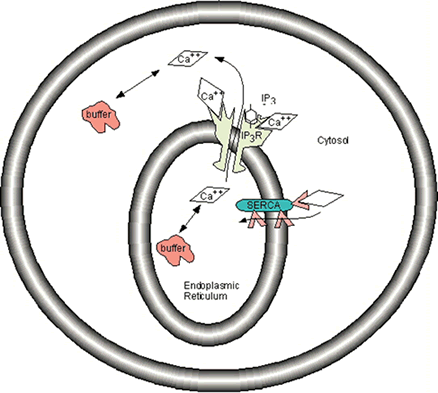
Figure 11: Calcium dynamics in soma compartment of model cell.
Computational modeling provides an innovative, yet practical method to evaluate the spatial extent, time course and interaction among second messenger pathways. Traditionally, the rates of individual reactions are assessed in biochemical experiments, and the end effect of neuromodulators are evaluated in neurophysiology experiments. Computational modeling is a technique that allows integration of the information obtained from these biochemical, pharmacological, and molecular biology experiments with the information obtained from electrophysiology and calcium imaging experiments. A computational model that includes both electrical and biochemical properties may be verified through comparison with independent physiological experiments. The resulting integrative model provides insight into mechanisms underlying neuromodulatory effects, and dynamics of neuronal activity; simulation experiments using the model generate testable hypotheses.
Several neural simulation software packages have the capabilities for modeling second messenger pathways. GENESIS ( Bower and Beeman, 1998 ), together with the Kinetikit ( Bhalla and Iyengar 2004a , 2004b ) and Chemesis ( Blackwell and Hellgren-Kotaleski 2002 ; http://www.gmu.edu/departments/krasnow/CENlab/chemesis.html ) libraries can model both deterministic and stochastic reactions and diffusion. NEURON ( Hines and Carnevale 1997 ) models deterministic and stochastic reactions and one-dimensional deterministic diffusion. XPPAUT can simulate any model for which mathematical equations can be written. The capabilities of several of these software packages are illustrated with simulation scripts for a short second messenger pathway, leading from metabotropic glutamate receptor activation to production of IP3. In addition, four scripts in Chemesis provide a step-by-step illustration of how to build a calcium dynamics model.
Keep track of molecule quantities and concentrations
-
Similar to compartment calculating voltage
-
Requires geometry/morphology values
-
length
-
radius
-
area of outer surface
-
area of inner surface (can be zero)
-
area of side surface
-
volume
-
-
rxnpool (Chemesis)
-
dC/dt = ∑ A - ∑ B C
-
A = change in quantity independent of present quantity
-
B = rate of change
-
Receives messages with quantities A and B from other objects (enzymes, reactions, also calcium influx)
-
-
conservepool (Chemesis)
-
C = Ctot - ∑Ci
-
Quantity is remainder after all other forms of molecule accounted for.
-
-
pool (Kinetikit)
-
dC/dt = ∑ A - ∑ B C
-
Or C = Ctot - ∑Ci (if flag is set to conserve)
-
Can also implement stochastic reactions
-
Calculate changes due to reactions
-
mmenz (Chemesis)
-
Use if MM assumptions are met
-
Fields: Km and Vmax
-
Inputs: Enzyme, substrate concentration
-
Calculates Vmax times [Enzyme] times substrate
-
Empirical feedback modification of enzyme activity can be added.
-
-
Enzyme (Chemesis)
-
Fields: Kcat, Kf, Kb
-
Inputs: enzyme, substrate quantity
-
Calculates amount of Enzyme-Substrate complex
-
Calculates change in product, enzyme, substrate
-
-
Enz (kinetikit)
-
Fields: Kcat, Kf, Kb
-
Inputs: enzyme, substrate quantity
-
Can implement stochastic reactions
-
-
reaction (Chemesis) or reac (kinetikit)
-
Fields: kf, kb
-
Inputs: substrates and products
-
Calculates:
-
forward rate constant times substrate molecules
-
backward rate constant times product molecules
-
-
CICR implements calcium release states
-
One element for each state
-
One of the elements may be conserved
-
Parameters (Fields)
-
'Forward' rate constants, α, β, γ
-
State vector, e.g. 001 for 1 Ca++ and 0 IP3 bound
-
Fraction of receptors in this state
-
Whether this element is conserved
-
-
Messages (Inputs) required:
-
IP3 concentration
-
Cytosolic Ca++ concentration
-
fraction of molecules in states that can transition to this state
-
rate constant governing transition from other states to this state
-
-
Calculates
-
Fraction of molecules in the state
-
CICRFLUX implements calcium release
-
Messages (inputs) required:
-
Calcium concentration of ER
-
Calcium concentration of Cytosol
-
Fraction of channels in open state, X
-
-
Parameters (Fields)
-
Permeability, P
-
Number of independent subunits, q
-
-
Calculates Ca flux = P*Xq (CaER-CaCyt)
Diffusion
-
Parameters (Fields)
-
Diffusion constant, D
-
-
Messages (Inputs)
-
Length, concentration, surface area from two reaction pools
-
-
Calculates
-
Flux from one pool to another
-
D SA Conc / len
-
Leak implemented using CICRFLUX
-
Messages (inputs) required:
-
Calcium of cytosol
-
Calcium of ER or EC space
-
Value of 1.0 instead of open state
-
-
Parameters (Fields)
-
Maximal Permeability (PL)
-
Hill coefficient (should be 1.0)
-
MMPUMP used for SERCA or PMCA Pump
-
Fields
-
Affinity
-
Power (exponent)
-
Maximum rate
-
-
Messages (inputs)
-
Concentration
-
-
Calculates flux due to pump
Integrating Calcium Mechanisms
-
RXNPOOL takes flux messages from various calcium sources
-
VDCC sends message CURRENT, with fields current and valence
-
Diffusion and release send message RXN2MOLES or RXN2, with fields difflux1 and difflux2, or fluxconc1 and fluxconc2, respectively
-
Mmpump sends message RXN0MOLES with field moles-out (to cytosol) or moles_in
-
Reactions send messages RXN0 - RXN2
-
Ca_concen
-
Simplest implementation of calcium
-
Fields
-
Time constant of decay
-
Minimum calcium
-
B = 1 / (z F vol): volume to produce 'reasonable' calcium concentration
-
-
Inputs
-
Calcium current
-
Note: Code of all the following is in genesis/src/concen after having installed GENESIS.
Concpool
-
Calcium concentration without diffusion
-
Fields: Shape and size
-
Inputs:
-
Buffer rate constants, bound and free
-
MMPump coefficients
-
Influx and outflux of stores
-
difshell
-
concentration shell. Has ionic current flow, one-dimensional diffusion, first order buffering and pumps, store influx
fixbuffer
-
Non-diffusible buffer (use with difshell)
Difbuffer
-
Diffusible buffer (use with difshell)
Augustine GJ, Charlton MP and Smith, SJ (1985). Calcium entry and transmitter release at voltage-clamped nerve terminals of squid. The Journal of Physiology 367, 163-181.
Berridge MJ (1987). Inositol triphosphate and diacylglycerol: Two interacting second messengers. Annu.Rev.Biochem. 56:159-193.
Bhalla US (2004a) Signaling in small subcellular volumes. I. Stochastic and diffusion effects on individual pathways. Biophys J 87:733-744.
Bhalla US (2004b) Signaling in small subcellular volumes. II. Stochastic and diffusion effects on synaptic network properties. Biophys J 87:745-753.
Bhalla US, Iyengar R (1999) Emergent properties of networks of biological signaling pathways. Science 283: 381-387.
Blackwell KT, Hellgren-Kotaleski J (2002) Modeling the dynamics of second messenger pathways. In: Neuroscience Databases. A Practical Guide (Kotter R, ed), pp 63-80. Boston: Kluwer Academic Publishers.
Bower JM, Beeman D (1998) The Book of Genesis: Exploring Realistic Neural Models with the GEneral NEural SImulation System (2nd edition). New York: Springer-Verlag.
DeSchutter E and Schmolen P (1998). Calcium Dynamics in Large Neuronal Models; in: Methods in Neuronal Modeling: From Ions to Networks, 2nd edition Koch C and Segev I (Eds.), MIT Press, Cambridge, MA.
De Young GW and Keizer J (1992). A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proceedings National Academy Sciences.USA 89: 9895-9899.
Enyedi A, Verma AK, Heim R, Adamo HP, Filoteo, AG, Strehler, EE, and Penniston, JT (1994). The Ca2+ affinity of the plasma membrane Ca2+ pump is controlled by alternative splicing. J.Biol.Chem. 269: 41-43.
Ermentrout B (2002) Simulating, Analyzing, and Animating Dynamical Systems: A Guide to XPPAUT for Researchers and Students, publisher: SIAM (Society for Industrial and Applied Mathematics).
Fujioka Y, Komeda M, and Matsuoka S (2000). Stoichiometry of Na+-Ca2+ exchange in inside-out patches excised from guinea-pig ventricular myocytes. J. Physiol 523 Pt 2:339-351.
Gale GD, Anagnostaras SG, Fanselow MS (2001) Cholinergic modulation of pavlovian fear conditioning: effects of intrahippocampal scopolamine infusion. Hippocampus 11: 371-376.
Gall D, Gromada J Susa I, Rorsman P, Herchuelz A, and Bokvist K. (1999). Significance of Na/Ca exchange for Ca2+ buffering and electrical activity in mouse pancreatic beta-cells. Biophys. J. 76:2018-2028.
Hines ML, Carnevale NT (2000) Expanding NEURON's repertoire of mechanisms with NMODL. Neural Comput 12: 995-1007.
Hines ML and Carnevale NT (1997). The NEURON simulation environment. Neural Comput. 1997 Aug 15;9(6):1179-209.
Kennedy, MB (1989). Regulation of neural function by calcium. Trends Neurosci. 12:417-420.
Levitan I and Kaczmark L (1997). The Neuron (3rd edition). Oxford University Press.
Leloup and Goldbeter (1999). Chaos and birhythmicity in a model for circadian oscillations of the PER and TIM proteins in drosophila. J Theor Biol. 1999 Jun 7;198(3):445-59.
Li, YX and Rinzel J, (1994). Equations for InsP3 Receptor-mediated [Ca2+]; Oscillations Derived from a Detailed Kinetic Model: A Hodgkin-Huxley Like Formalism. J. Theor. Biol. 166:461-473.
Nicholls JG, Martin AR, Wallace BG and Fuchs PA (2001). From Neuron to Brain (4th Edition).Sinauer, MA.
Powers DL (1979). Boundary Value Problems (2nd edition), Academic Press, London.
Tang, Y and Othmer HG (1994). A model of calcium dynamics in cardiac myocytes based on the kinetics of ryanodine-sensitive calcium channels. Biophysical.J. 67: 2223-2235.
Wichmann T, DeLong MR (1998) Models of basal ganglia function and pathophysiology of movement disorders
License
Any party may pass on this Work by electronic means and make it available for download under the terms and conditions of the Digital Peer Publishing License. The text of the license may be accessed and retrieved via Internet at http://www.dipp.nrw.de/lizenzen/dppl/dppl/DPPL_v2_en_06-2004.html